Ratios of Trigonometric sides are known as TRIGONOMETRIC RATIOS.
In Trigonometry, Trigonometric sides are given special significance. So the ratio’s of these sides automatically became important.
TRIGONOMETRIC SIDES
PERPENDICULAR
BASE
HYPOTENUSE
We can make 6 combinations of ratio’s based on above mentioned 3 Trigonometric sides. [Try if you can make more than 6 combinations & comment below]
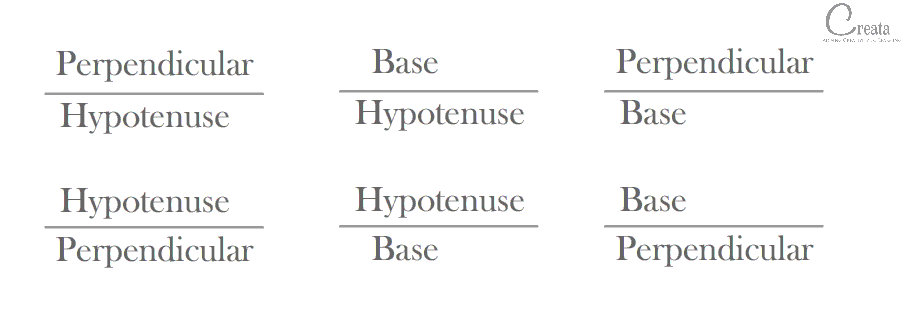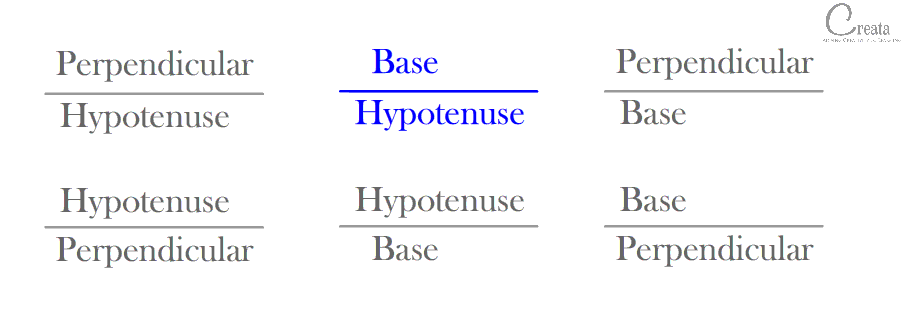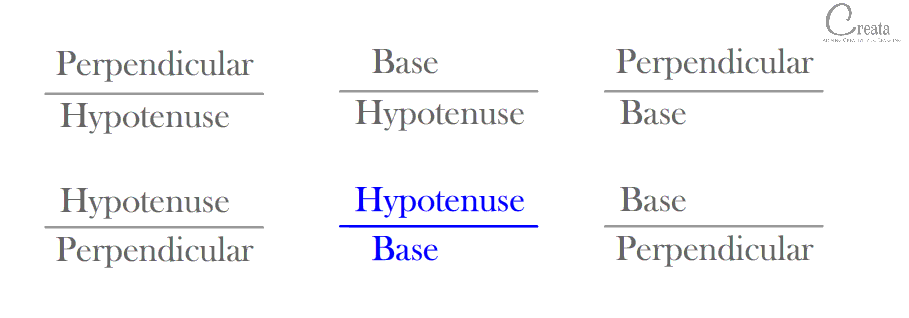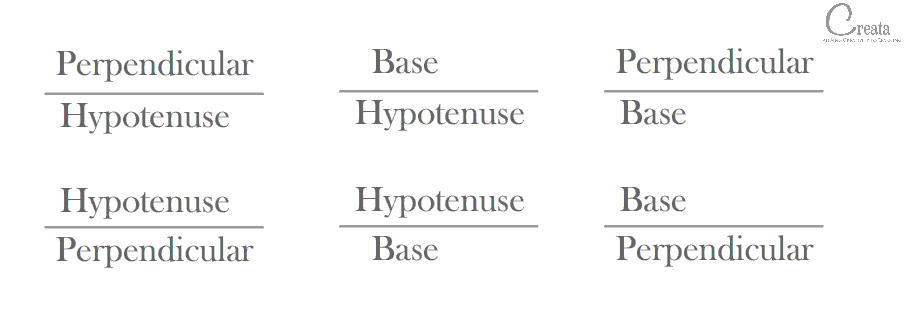
These 6 ratio’s are TRIGONOMETRIC RATIOS. Special names have been allotted to these ratio’s. Which are:
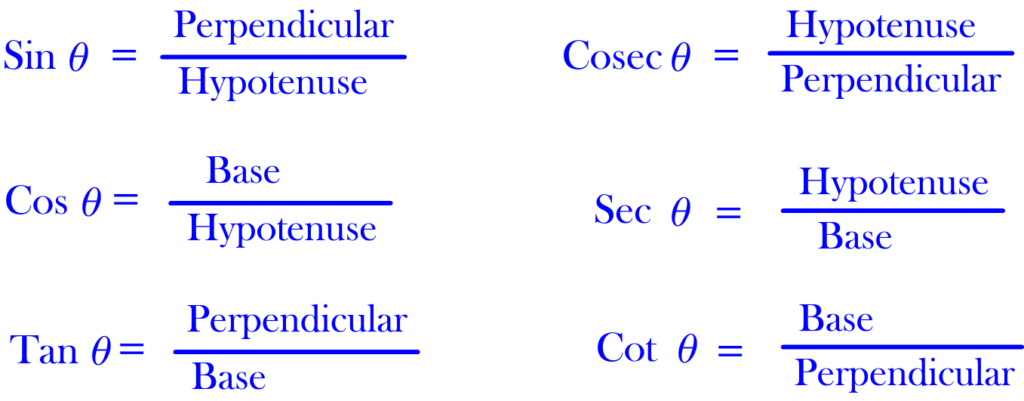
Previously, we have understood that Trigonometric sides are w.r.t to some angle, which we have called as Trigonometric angle. So here also, Trigonometric ratio’s are w.r.t Trigonometric angle. So \theta , as Trigonometric angle, is placed with Trigonometric ratios.
You will observe that Cosec, Sec & Cot are reciprocal of Sin, Cos & Tan respectively. Refer details in post of “Relation among Trigonometric Ratio’s”.
So, Just remember the Trigonometric ratios of Sin, Cos & Tan only. Rest will come automatically, by doing the reciprocal.
HOW TO APPROACH QUESTIONS
- We can calculate Trigonometric Ratio’s, if we know the 3 sides of a right-angle triangle.
- If only 2 sides are given. Find the missing side with help of Pythagorean theorem.
- Remember the triplets of Pythagorean theorem. [(3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25) etc].
- Once we know the 3 sides, identify the Trigonometric sides (Perpendicular, Base & Hypotenuse). Same we have already covered in previous post.
- Once, you know the 3 Trigonometric side, apply the formulas to get Trigonometric Ratio’s.
EXAMPLES
Q1) Find the Trigonometric Ratio’s Sin \theta , Cos \theta & Tan \theta for the given triangle ABC.
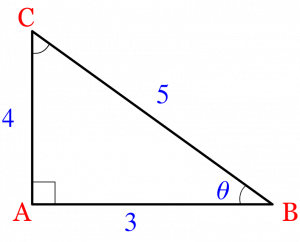
Firstly, we have to identify the Trigonometric sides Perpendicular, Base & Hypotenuse. Refer below animation for the same.
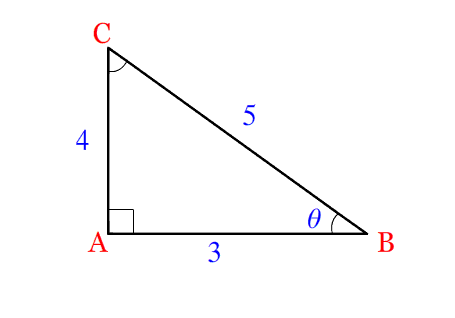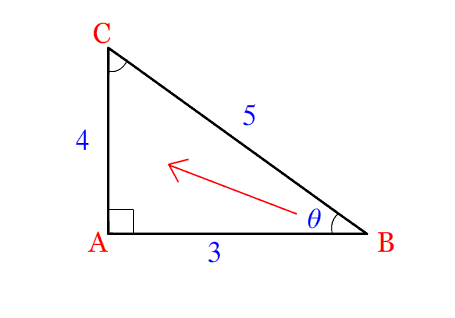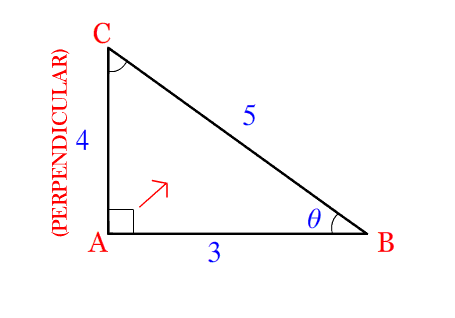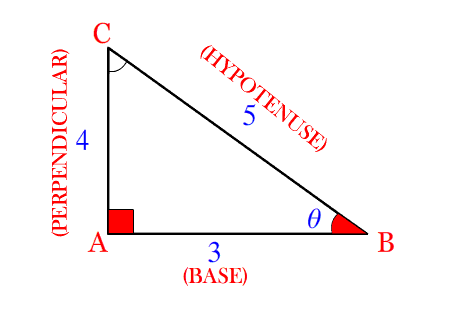
We got,
Perpendicular = 4 (Side Opposite to Trigonometric angle \theta )
Base= 3 (Side between 90 Degree & Trigonometric angle \theta )
Hypotenuse = 5 (Side opposite to 90 Degree angle)
Click here to know, How to identify Trigonometric Sides.
Once, we know the 3 sides, we can use formula’s of Trigonometric Ratio’s.

Q2) Find the Trigonometric Ratio’s Sin \theta , Cos \theta & Tan \theta , for the given triangle PQR.

Firstly, we have to identify the 3rd missing side, then only, we can proceed further.
We will use Pythagoras, to find the 3rd missing side.
PQ 2 + QR 2 = PR 2
52 + 12 2 = PR 2
PR = 13
We got all the 3 sides.
Now, we have to identify Perpendicular, Base & Hypotenuse.
PQ is Perpendicular, as it is side opposite to Trigonometric angle \theta .
PQ = Perpendicular = 4
QR is base, as it is between 90 degree angle & Trigonometric angle \theta .
QR = Base= 12
PR is Hypotenuse, as it is opposite to 90 degree \theta .
PR = Hypotenuse = 13
Once, we got the 3 sides, we will apply Trigonometric Ratios Formulas.

Question for you:
Q) Find the Trigonometric Ratio’s Sin \theta , Cos \theta & Tan \theta , for the given triangle ABC.


